Nonamed Develog
[TIL][240729] Tree 본문
새로 알게 된 점은 무엇인가?
계층형 자료구조의 특징
- Originated from one source.
- One node is propagated into several nodes.
*propagate: to produce a new plant using a parent plant. - No cycle path.
트리 Tree
비선형 구조. 원소 간 계층 관계를 가지며, 상위 원소에서 하위 원소로 내려가면서 확장되는 "나무 모양" 구조
- There is a special designated node call the root.
- Every pairs of connected nodes are in parent-child relationship.
- There is no cycle in the nodes.
- Reculsively defined self-referential date structure
용어 정리

- Node(or Vertex): 트리를 구성하는 기본 요소
- Edge: 간선. 노드와 노드 간의 연결(드물게 root와 leaf 사이의 모든 노드를 일컫기도 함)
- Root node: 트리의 꼭대기에 있는 노드
- Leaf node: 더 이상 자 노드가 없는 최하위 노드
- Internal node: 적어도 하나의 자식이 있는 노드
- Parent node: 해당 노드 바로 위에 있는 부모 노드
- Child node: 해당 노드 바로 아래에 있는 자식 노드
- Sibling node: 같은 부모를 갖는 노드들의 집합
- Ancester node: 간선을 따라 루트 노드까지 가는 경로상에 있는 모든 노드
- Descendent node: 루트 노드로부터 간선을 따라 특정 노드까지 경로상에 있는 모든 노드
- Subtree: 주어진 노드의 모든 하위 목록. 부모 노드와 연결된 간선을 끊었을 때 생성되는 트리
- Degree of a node: 특정 노드가 가지고 있는 자식 노드의 수(차수)
- Degree of tree: 트리 내에 있는 노드들의 차수 중 가장 큰 값
- Depth of a node(Level): 루트에서 특정 노드까지의 간선의 수
- Depth of a tree: 루트에서 가장 깊은 노드까지의 간선 수
- Width of a tree: 각 레벨에서 노드의 최대 노드
이진트리 Binary Tree
- A tree whose degree is 2
- The maximum degree of its node is 2
- n개의 노드 가질 때 간선의 수? ➡️ n-1
- i번째 레벨의 최대 노드 수?
➡️ 2^(i-1)(root level이 1인 경우) / 2^i(root level이 0인 경우) - O(N) - 깊이가 k인 이진트리의 최대 노드 수?
➡️ 2^k-1(root level이 1인 경우) / 2^(k+1)-1(root level이 0인 경우) - O(logN) - 깊이가 k인 이진 트리의 최소 노드 수? ➡️ k+1
이진 트리의 종류

- 정 이진 트리 Full Binary Tree
- 모든 노드가 0개 또는 2개의 자식 노드를 갖는다.
- 노드의 수 = 2^(depth) - 1 - 완전 이진 트리 Complete Binary Tree
- 마지막 레벨을 제외한 모든 노드가 가득 차야 한다.
- 마지막 레벨의 노드는 전부 차 있지 않아도 되지만 왼쪽은 채워져야 한다. - 포화 이진트리(Perfect Binary Tree)
- Full Binary Tree 이자 Perfect Binary Tree
- 모든 리프 노드의 레벨이 동일하고 모든 레벨이 가득 채워져 있다.
이진 트리 순회
- Search(*탐색) == Traversal(*순회)
- 어떤 값이 주어졌을 때 해당 값이 일치하는 노드가 있는지 탐색(모든 노드를 확인해야 함) - DFS(Depth-First Search): 트리의 한 경로를 끝까지 탐색한 후 다른 경로를 탐색한다.
- 스택(stack) 또는 재귀(recursion)를 이용하려 구현할 수 있다. - 3가지 순회하는 방법이 존재한다. (Preorder / Inorder / Postorder)
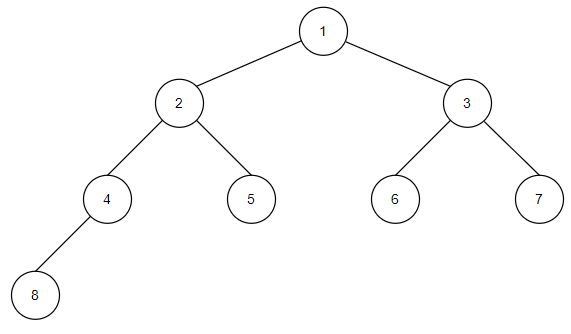
- 트리의 구조: 3가지 순회 방법에 앞서 트리의 구조를 구현하면 아래와 같다.
class Node(object):
def __init__(self, item):
self.item = item # 루트(노드)가 갖는 값을 저장
self.left = self.right = None # 각 루트의 자식 노드
class BinaryTree(object):
def __init__(self): Node 원소를 초기화
self.root = None # 빈 루트- 전위 순회 Preorder Traversal: 루트 ➡️ 왼쪽 ➡️ 오른쪽
def preorder(self):
def _preorder(node):
print(node.item, end=' ') # 제일 먼저 루트를 프린트한다.
if node.left:
_preorder(node.left)
if node.right:
_preorder(node.right)
_preorder(self.root)순회: 1-2-4-8-5-3-6-7
- 중위 순회 Inorder Traversal: 왼쪽 ➡️ 루트 ➡️ 오른쪽
def inorder(self):
def _inorder(node):
if node.left:
_inorder(node.left)
print(node.item, end=' ') # 중간에 프린트가 있다
if node.right:
_inorder(node.right)
_inorder(self.root)순회: 8-4-2-5-1-6-3-7
- 후위 순회 Postorder Traversal: 왼쪽 ➡️ 오른쪽 ➡️ 루트
def postorder(self):
def _postorder(node):
if node.left:
_postorder(node.left)
if node.right:
_postorder(node.right)
print(node.item, end=' ') # 마지막 프린트
_postorder(self.root)순회: 8-4-5-2-6-7-3-1
- 레벨 순회 Level Traversal
- BFS(Breadth-First Search)로 트리를 레벨순으로 노드를 방문하는 방법
- 큐(Queue)를 이용해 구현할 수 있다.
from collections import deque
def levelorder(self):
q = deque([self.root])
while q:
node = q.popleft()
print(node.item, end=' ')
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)순회: 1-2-3-4-5-6-7-8
무엇을 느꼈고 내일은 무엇을 할까?
과제로 나온 트리 순회 문제를 풀이 후 리스트를 이용해 2진 트리 구현
'WHAT I LEARN > TIL' 카테고리의 다른 글
| [TIL][240731] 약수, 소수, 시간복잡도 그리고 에라토스테네스의 체 (0) | 2024.07.31 |
|---|---|
| [TIL][240730] CS: The Python Libraries for ML and AI (0) | 2024.07.30 |
| [TIL][240726] 소프트웨어 설계 나머지 공부 (0) | 2024.07.26 |
| [TIL][240725] Search, Retrieve, 2차원 배열, CS 개념 (0) | 2024.07.25 |
| [TIL][240724] 자료구조(Data structure), 배열(Array), 연결 리스트(Linked list) (1) | 2024.07.24 |




